Table of Contents
ToggleIntroduction to Solid State Physics
Crystal Structure
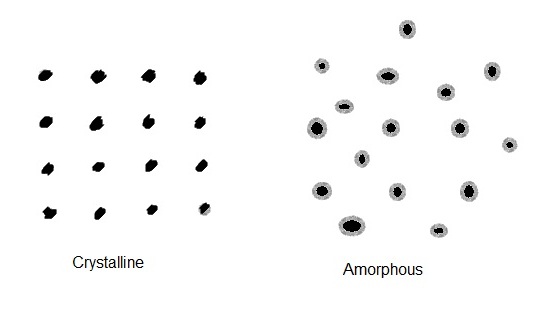
Crystalline nature of matter:
If the atoms or molecules in a solid are arranged in some regular fashion then it is known as crystalline. When the atoms or molecules in a solid are arranged in a irregular fashion then it is known as amorphous.
Crystal:
A crystal is a solid composed of a periodic array of atoms i.e. a representative unit is repeated at regular intervals along array and all directions. Crystallography: The study of the geometric form and other physical properties of crystalline solids by using x-rays, electron beams and neutron beams etc., called as crystallography.
Differences between crystalline and amorphous solids:
| Crystalline solids These have a regular arrangement of particles in the solid. These have different physical properties (thermal conductivity, refractive index, etc) in different directions i.e. These are anisotropic substances. All bonds in crystalline solids are equally strong due to their symmetry. These have very sharp melting point. | Amorphous solids These have a completely random arrangement. These have same physical properties in all directions All bonds in amorphous solid are not equally strong. These donot have sharp melting point. |
Space lattice: Crystals made up of regular and periodic three dimensional arrangements in space called the crystal structure. The periodic arrangement of atoms in a crystal is called the lattice. There is a group of several atoms or ions at each lattice point. This group is called as basis. So the crystal structure is formed when a basis of atoms is formed when a basis of atoms is attached identically to each lattice point.
Basic point in Introduction to Solid State Physics
Lattice + basis = crystal structure
Unit cell: A unit cell is the smallest geometric figure the repetition of which gives the actual crystal structure.
The fundamental elementary pattern of minimum number of atoms, molecules or group of molecules which represent fully all the characteristics of the crystal is call unit cell.
The unit cell is a parallelepiped formed by the basis vectors a,b,c as concurrent edges and including angles a, b, g between b and c, c and a and a and b respectively as shown in figure.
Crystal lattice: The entire lattice structure of a crystal is found to consist of identical blocks or unit cells. The lattice is known as crystal lattice.
Elements of symmetry: following three are the main elements of symmetry.
1. Axes of symmetry 2. Planes of symmetry 3.Centre of symmetry
| 1. Axes of symmetry: If the crystal occupies identical positions during its rotation through 360°, then the axis of rotation is known as axis of rotation. In the case of a cube four identical positions in one complete rotation. Therefore, the crystal has four fold axis of symmetry for each 90° (360°/n=4) rotation. | |
| 2. Plane of symmetry: The planes which cut a crystal into two halves so that each half is a mirror image of the other half, then the plane is known as plane of symmetry There are three planes can easily be constructed, each parallel to different faces of the cube. | |
| There are 6 diagonal planes can easily be constructed as shown \For a cube, there are ‘9’ planes of symmetry. | |
| 3. Centre of symmetry: This refers to a point in the crystal such that a line drawn from any lattice point in the crystal through this point gives equal distance. The cubic has only one such centre of symmetry. | |
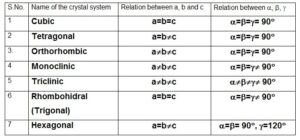
| Crystal system: On the basis of the length and directions of the axes of the symmetry, all the crystals may be classified into following seven systems. | |
| 1. Cubic system: In this crystal all the three lengths of the unit cell are equal and at right angles to each other. i.e. a=b=c and a=b=g = 90° ex: diamond, NaCl, CaF2, etc. | |
| 2. Tetragonal system: In this system, two lengths of the unit cell are equal while the third one is longer. The three axes are perpendicular. a=b¹c and a=b=g = 90° Eg: NiSO4, SnO2. | |
| 3. Orthorhombic system: In this system a¹b¹c but they are at right angles to each other i.e. a=b=g = 90° Eg. KNO3, BaSO4, Mg2SiO4, carnallite | |
| 4. Monoclinic system: It is also known as monosymmetric system. In this type of crystals, a¹b¹c and a=b= 90°¹g Eg. Na2SO4, FeSO4, Borax | |
| 5. Triclinic system: In this system, neither of the three lattice parameters nor their angles are equal. i.e. a¹b¹c and a¹b¹g Eg. CuSO4, K2Cr2O7 | |
| 6. Rhombohedral system: (trigonal) In this system a=b=c and a=b=g ¹ 90° Eg. Quartz, calcite, | |
| 7. Hexagonal system: In this system a=b¹c and a=b= 90°, g = 120° Eg. SiO2, AgI |
| S.No. | Name of the crystal system | Relation between a, b and c | Relation between a, b, g |
| 1 | Cubic | a=b=c | a=b=g= 90° |
| 2 | Tetragonal | a=b¹c | a=b=g= 90° |
| 3. | Orthorhombic | a¹b¹c | a=b=g= 90° |
| 4 | Monoclinic | a¹b¹c | a=b=g¹ 90° |
| 5 | Triclinic | a¹b¹c | a¹b¹g¹ 90° |
| 6 | Rhombohidral (Trigonal) | a=b=c | a=b=g¹ 90° |
| 7 | Hexagonal | a=b¹c | a=b= 90°, g=120° |
Bravais space lattices:
Bravais showed that there are 14 ways of arranging points in space lattice called the Bravais lattice. In case of a cubic system, there are 3 Bravais lattice. These are
1. Simple cubic or primitive cubic 2. Face centered cubic (fcc)
3. Body centered cubic (bcc)
| 1. Simple cubic: There is one lattice point at each of eight corners of the unit cell. The share of each lattice point to the cubic lattice = 1/8 \Number of lattice points in unit cell = 1/8 x 8 = 1 i.e. there is only one lattice point per unit cell | |
| 2. Face centred cubic: There is one lattice point at each of the eight corners and one lattice point at the centers of each of the six faces of the cubic cell. Total number of corners lattice points in unit cell 8 x (1/8) = 1 Total number of face centred lattice points in unit cell = 6 x ½ = 3. Total number of lattice points concerned with unit cell = 1+3=4 | |
| Body centred cubic: There is one lattice point at each of the eight corners and one lattice point at the centre of each cell. \Total number of corner lattice points per unit cell 8 x (1/8) = 1 Total number of body centred lattice points per unit cell = 1 \Total number of lattice points concerned with unit cell = 1 + 1 = 2 |
Miller indices: The miller indices are the three smallest possible integers which have the same ratio as the reciprocals of the intercepts of the plane concerned on the three axes.
The Miller indices of a plane is defined as the reciprocals of the intercepts which the plane makes with the axes when reduced to smallest numbers.
Rules for finding Miller indices:
1. First of all determine the intercepts of plane on the three co-ordinate axes.
2. Secondary take the reciprocals of these intercepts.
3. Lastly, reduce the reciprocals into whole number by multiplying each reciprocal by number obtained after taking L.C.M. of denomination.
These Miller indices are represented by (h,k,l)
Diamond structure: The diamond structure is a combination of two inter penetrating face centered cubic lattice. Each atom in this structure has four nearest neighbours, occupying the corner point of a regular tetra hedron to which it is bonded by strong covalent bonds. The diamond structure is loosely packed since each atom has only 4 nearest neighbours.
The entire diamond lattice is constructed of tetrahedral units. Unit cell of diamond structure contains 18 atoms. But non of atoms in a unit cell of diamond structure is 8.
Zinc blende structure: The zinc blende (Zns) structure as shown in figure. The bonding is tetral hedron bonding structure with other atoms.
Structure of CsCl: This crystal has simple cubic structure with CS+ and Cl– ions as the basis. The unit cell of CsCl lattice is shown in figure.
In the figure, Cs+ ions are situated at the corners of the cubic cell and Cl– ions at the body centre or vice versa.
The coordination number for same kind of ions is 6 and the nearest neighbour distance is a lattice constant. The co-ordination number for opposite kind of ions as 8 and the nearest neighbour distance is
Sodium chloride structure: The sodium chloride structure is shown in figure. In this crystal the bond is ionic bond, it has the simple cubic structure with ions of sodium (Na) and chlorine (Cl) arranged alternatively at the corners of the cube. In terms of Bravais lattice, NaCl is a face cantered cube. In this crystal each ion is surrounded by six nearest neighbours of the same kind.